巡回セールスマン問題
巡回セールスマン問題とは、都市の集合と各2都市間の移動コスト(たとえば距離)が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る巡回路のうちで総移動コストが最小のものを求める(セールスマンが所定の複数の都市を1回だけ巡回する場合の最短経路を求める)組合せ最適化問題の事です。
警備業にも法で定められた巡回指導が存在し、現場ごと・警備員ごとに実施する必要があるので件数をこなすには、ある程度の効率を最適化しなければいけない。
まず出発到着地点をSとし、巡回場所がa,bの2か所だとします。
巡回ルートは以下の2通りです。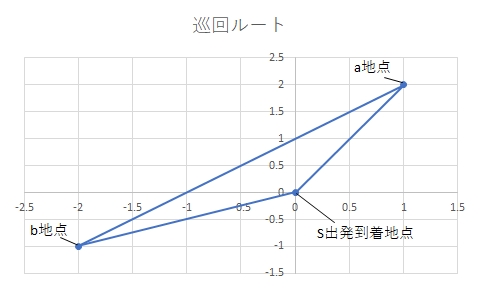
巡回ルート1
S→a→b→S
巡回ルート2
S→b→a→S
どちらのルートも方向が逆なだけで、移動距離に差は生じません。
次に巡回場所cが追加され3か所になると、どうなるでしょうか?
巡回ルートは一気に6通りまで増えます。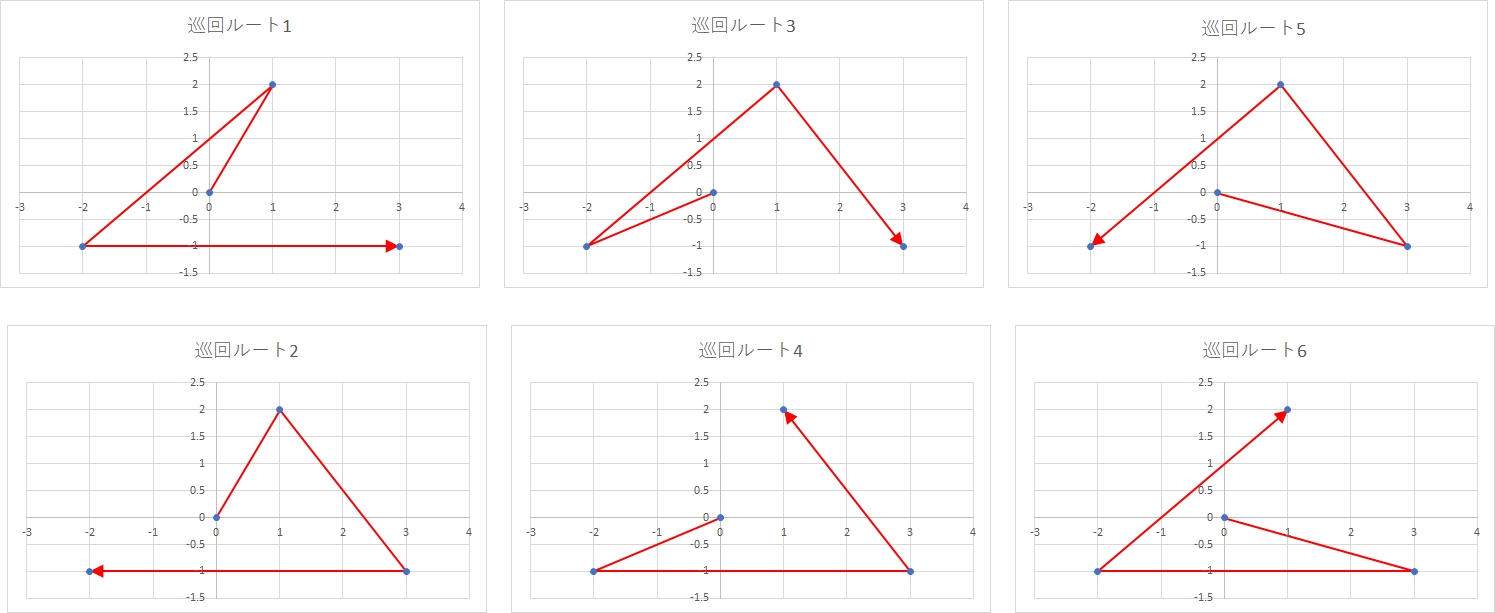
巡回ルート1
S→a→b→c→S 移動距離:14.64098632
巡回ルート2
S→a→c→b→S 移動距離:13.07768723
巡回ルート3
S→b→a→c→S 移動距離:13.2465376
巡回ルート4
S→b→c→a→S 移動距離:13.07768723
巡回ルート5
S→c→a→b→S 移動距離:13.2465376
巡回ルート6
S→c→b→a→S 移動距離:14.64098632
移動距離は直線の場合ピタゴラスの定理で算出すると、巡回ルート2,4に最適化される。
巡回ルートの組み合わせは、
巡回場所nの階乗(n!)
となる。巡回場所が4か所になると突如4!=24通りにもなる。
ここで巡回ルート1,6と巡回ルート2,4と巡回ルート3,5は共に逆回りなので移動距離は同じであるから移動距離の組み合わせは、
巡回場所nの階乗の半分(n!/2)
となる。仮に巡回場所が10か所だとすると、10!/2=1,814,400通りもの組み合わせになり人間の勘だけでは最適化不可能だ。
お勧めツール
ここまでが「巡回セールスの問題」になります。
現実的には普通に4~5か所の巡回指導が行われますが、移動距離を最適化して巡回ルートを検討しますか?と言われるとまず無いでしょう。
実際は営業であれ巡回指導であれ移動距離の最適化は、さほど重要ではなくそれ以外の要素のほうが重要であることが多い。
一番重要な要素は相手と会うことなので、こちらの事情よりも相手の都合を考慮するほうが重要になる。結局相手と会えなければ何の意味もないわけだし、後日巡回しなければならないので結果的に移動距離は伸びてしまいます。
営業マンや巡回指導員はどのようにして巡回ルートを決定するのでしょうか?
基本、適当です。
綿密な計画を立てたところで様々なイレギュラーが発生するので、あまり役に立ちません。結局”行き当たりばったり”なのが現実です。
そうであるなら、まずは移動距離を最適化するべきです。
巡回セールスマン問題の解を求める方法について今では幾つかのツールが存在します。
お勧めなのは、Google Mapの巡回セールスマン問題が便利です。
他にスマートフォン用のアプリもいくつか存在します。活用してみましょう。
いづれにせよ便利な時代になりましたね。
